Leonhardo, Euler (Eulero). Introductio in analysin infinitorum. Lugduni, Apud Bernuset, Delamolliere, Falque & Soc., 1797.

€3900.00 (In Stock)

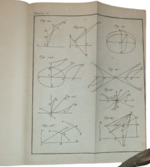
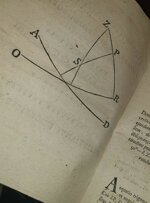
Lugduni, Apud Bernuset, Delamolliere, Falque & Soc., 1797. 2 tomi rilegati in 1 vol. in-4° (23,3 cm x 18,4 cm). Pp. XVI, 320; (2), 398. Con 1 grande “Tabula” più volte ripiegata tra le pp. 276 e 277 del 1° vol e 16 grandi tavole più volte ripiegate in fine. Segnatura: [ast.]-2[ast.]4, A-2R4; [p]1, A-3D4 (-3D4 bianca). Solida e bella legatura ottocentesca in mezza pelle blu, autore e titolo impressi in oro sul dorso ornato da fregi geometrici e romantici dorati in testa ed al piede. Testatine e finalini incisi. Qualche rara ed insignificante ossidazione marginale, peraltro esemplare in ottimo stato di conservazione.

Bella ed apprezzata edizione di una delle opere più famose nella storia della matematica analitica che segnò una rivoluzione in questa branca della matematica, una materia che fino ad allora non era mai stata presentata in modo così generale e sistematico. Il famoso matematico svizzero, il più grande del Settecento ed uno dei massimi della storia, fu allievo di Johann Bernoulli e in seguito si trasferì a San Pietroburgo per insegnare matematica e fisica. 

“Nella sua Introduzione all’ analisi matematica, Eulero fece per l’ analisi moderna ciò che Euclide aveva fatto per la geometria antica” (PMM). L’ Introduzione agli Infinitesimali stabilisce “la funzione, qui appare per la prima volta la definizione di funzione matematica,  come concetto fondamentale su cui si fonda l’ intera costruzione matematica”.   “Contiene un’ esposizione di algebra, trigonometria e geometria analitica, sia piana che solida, una definizione dei logaritmi come esponenti e importanti contributi alla teoria delle equazioni.” (PMM, 196). In algebra, Eulero si concentra in particolare sullo sviluppo di varie funzioni in serie e sulla somma di serie date; dimostra esplicitamente che una serie infinita non può essere utilizzata in modo affidabile se non è convergente. 

Carl Benjamin Boyer nelle sue lezioni al Congresso Internazionale dei Matematici del 1950 definì gli Elementi il ​​principale libro di testo dell’ antichità e l’ Introductio “il principale libro di testo dei tempi moderni”. Boyer scrisse anche: “L’ analisi di Eulero si avvicina alla disciplina ortodossa moderna, lo studio delle funzioni mediante processi infiniti, in particolare attraverso serie infinite; quella che prenderà il nome di Formula di Eulero diventerà  una formula fondamentale nel campo dell’ analisi complessa”. Fu anche il primo a discutere l' equazione di secondo grado in tre variabili e a classificare le superfici da essa rappresentate. Il lavoro di Eulero sulle serie infinite culminò nella creazione della teoria degli integrali definiti, noti come integrali euleriani. Sviluppò ulteriormente il calcolo delle differenze finite e stabilì il teorema delle funzioni omogenee. 

Per quanto riguarda la trigonometria, sviluppa l’ idea del suo maestro Johann Bernoulli secondo cui la trigonometria è una branca dell’ analisi e non una semplice appendice dell’ astronomia o della geometria; Eulero introdusse le abbreviazioni oggi in uso per le funzioni trigonometriche, oltre a buona parte della simbologia matematica tuttora in uso, e sottolineò la relazione tra funzioni trigonometriche ed esponenziali. La seconda parte dell’ Analysin infinitorum si concentra sulla geometria analitica, in cui l’ autore studia curve algebriche, cubiche, quartiche e di altro tipo. Esamina inoltre quali superfici sono rappresentate dall’ equazione quadratica generale in tre variabili e come possono essere distinte l’ una dall’ altra (cfr. Walter William Rouse Ball,  History of Mathematics). È sulla base dell’ opera di Eulero che Lagrange svilupperà la sua ricerca; le equazioni differenziali formulate e studiate da Eulero, una base della meccanica classica, furono studiate per primo proprio dal celebre matematico torinese Joseph-Louis Lagrange nel suo trattato Mécanique Analytique.

Bibliografia: Cantor, III, 699; Davis, 48; DSB, IV, 476; Eneström, 101/(2) & 102/(2); Hjalmar, 43; Honeyman, 1066; Rider, 148; Smith, History, I, 522; Norman, 732. Cfr. Cassina, Calcolo numerico, p. 438; Enriques, Gli Elementi d’ Euclide e la critica antica e moderna, VII, P. 340; Schubring, Conflicts Between Generalization, Rigor, and Intuition, p. 371.

Christian Friedrich, Rüdiger. Ad audiendam orationem professionis philosophiae extrordinariae adeundae caussa die III. Martii A. C. M. DCC. XCII. De effectu refractionis in ortum et occasum stellarum computando. Lipsiae, Ex Officina Klavbarthia, [1792].

NewCondition € 1300.00
In Stock

Vitruvio. Marco Vitruvio Pollione. (trad. Daniele Barbaro) I dieci libri dell’ architettura…tradotti, & commentati da Monsig. Daniel Barbaro Patriarca d’ Aquileia, da lui riveduti, & ampliati. In Venetia, Appresso Alessandro de’ Vecchi, 1629.

NewCondition € 1900.00
In Stock

Valentino, Ceccato (Cecato). Il moto della Terra dimostrato contrario alla fede ed alla ragione in sei lettere scritte ad un amico dal r.d. Valentin Cecato prete della Chiesa di S. Geremia. In Venezia, Nella Stamperia Fenzo, 1783.

NewCondition € 2500.00
In Stock

Stefano, Degli Angeli. De Infinitorum spiralium spatiorum mensura, opusculum geometricum. Venetiis, Apud Ioannem La Noù, 1660.

NewCondition € 2100.00
In Stock

G.P., Gallucci. Della Fabrica & uso di un novo stromento fatto in quattro maniere per fare gli horologi solari ad ogni latitudine, Con tutte le sorti di hore, che si usano [...].In Venetia, appresso Gratioso Perchacino, 1590.

NewCondition € 1750.00
In Stock

Manoscritto del '700. Elementorum Physices.

NewCondition € 950.00
In Stock

Giacomo, Barozzi da Vignola. Regola delli cinque ordini d’ architettura (insieme con: "Alcune opere d'architettura di Iacomo Barotio da Vignola raccolte et poste in luce da Francesco Villamena" . (S.l.) Roma, presso Carlo Losi, 1773.

NewCondition € 1200.00
In Stock

Prof. Corrado, Segre. Sulle Varietà Cubiche dello Spazio a quattro dimensioni e su certi sistemi di rette e certe superficie dello spazio ordinario. 1887.

NewCondition € 170.00
In Stock

Edmund, Landau. Problemi di Landau. “Teoria dei Numeri” “Zahlentheorie”. 1906-1908.

NewCondition € 1750.00
In Stock

Armando, Chiellini. Sulla Serie. 1931.

NewCondition € 380.00
In Stock

Carlo, Sigonio. Historiarum de regno Italiae Libri Quindicem. Ad Illustriss. Atqu. Excell. D. Iacobum Boncompagnum, Generalem. S.R.E. Gubernatorem. Qui libri historiam ab anno DLXX usque ad vsque ad MDD continent. Venetiis, Apud Iordanem Zilettum, 1574.

NewCondition € 1300.00
In Stock

Giambattista, Vico. Principj di scienza nuova […] d’ intorno alla comune natura delle nazioni. In Napoli, Nella Stamperia Muziana, A spese di Gaetano, e Steffano Elia, 1744.

NewCondition € 1900.00
In Stock

Josè-Raul, Capablanca. My chess career. London, Bell and Sons Ltd., 1920.

NewCondition € 520.00
In Stock

Jean Antoine, NOLLET. Saggio intorno all' Elettricità de' corpi. […] Aggiuntevi alcune Esperienze ed Osservazioni che illustrano l istessa materia, del Sig. Guglielmo Watson.

NewCondition € 600.00
In Stock

Benjamin, Franklin. Expériences et Observations sur l'Electricité faites à Philadelphie en Amérique. A Paris, chez Durand, 1752.

NewCondition € 1800.00
In Stock

Prof. Corrado, Segre. Le Coppie di Elementi Imaginari nella Geometria Proiettiva Sintetica. 1886.

NewCondition € 170.00
In Stock

Johann Joachim, Becher. Physica Subterranea profundam subterraneorum genesin, e principiis hucusque ignotis, ostendens. (insieme:) Specimen Beccherianum , sistens Fundamenta, Documenta, Experimenta, Quibus [...]. Lipsiae, Ex Officina Weidmanniana, 1738.

NewCondition € 1700.00
In Stock

Alessandro, Achillini Bolognese. Aristotele. Expositio primi physicorum. [Bononiae], Impresseum Hieronymum de Benedictis Cive bononiensem, Anno 1512.

NewCondition € 3200.00
In Stock

Saggio Sul Nitro o Salnitro, Sua Natura, Produtione, Cottura e Fabricazione. 1700.

NewCondition € 850.00
In Stock

Carmine, Vincenti. Istituzioni di Epidesmologia. Napoli, Dai torchi di Luca Marotta, 1817.

NewCondition € 890.00
In Stock

Giovanni Francesco, Pivati. Riflessioni fisiche sopra la medicina elettrica. In Venezia, Presso Benedetto Milocco: si vendono da Lorenzo Baseggio in Campo a S. Bartolomeo, 1749.

NewCondition € 850.00
In Stock

Edna, Yost. Frank and Lillian, Gilbreth. Partners for Life. New Brunswick, Rutgers University Press, 1949. Autografato.

NewCondition € 500.00
In Stock

San Tommaso, d’ Aquino. Aristotele. S. Thomae Aquinatis in quatuor libros Aristotelis De Coelo, et Mundo Commentaria. Venetiis, Apud Hieronymum Scotum, 1562.

NewCondition € 1500.00
In Stock

Le Petit bijou des enfans. Année 1816. Paris, Marcilly, [1815].

NewCondition € 1300.00
In Stock

Giuseppe, TORRUBIA. (José, Torrubia). La Gigantologia Spagnola vendicata…Dedicata all' Ill.mo, ed Ecc.mo Signore, Monsignore D. Alfonso Clemente de Arostegui.

NewCondition € 2300.00
In Stock

Josepho, Cantelio (Pierre Joseph, Cantel). De Romana Repubblica sive de re militari & civili romanorum ad explicandos scriptores antiquos. Utrejecti (Utrecht), apud Gulielmum Vande Water, 1707.

NewCondition € 900.00
In Stock

Jean Louis Eugene, Lerminier. Introduction generale a l’ histoire du droit Bruxelles, Librairie de jurisprudence de H. Tarlier, 1836.

NewCondition € 100.00
In Stock

Dante, Alighieri. (a cura di Jacopo, Giuliani. Giambattista, Giuliani.) La Commedia di Dante Allighieri raffermata nel testo giusta la ragione e l’ arte dell’ autore da Giambattista Giuliani. Firenze, Successori Le Monnier, 1902.

NewCondition € 110.00
In Stock

Serge Lifar a l’ Opera, défini par Paul Valery, parlé par Jean Cocteau, vécu par Serge Lifar Paris, Thibault de Champrosay, 1943.

NewCondition € 130.00
In Stock

Baldassarre, Castiglione. Il libro del cortegiano. In Firenze, Per li heredi di Philippo di Giunta nell’ anno 1531 del mese d’ Aprile.

NewCondition € 3900.00
In Stock

Angelo, Brofferio. Storia del Piemonte. Dal 1814 ai giorni nostri. Torino, Stabil. Tipogr. di Aless. Fontana, 1849-1852.

NewCondition € 300.00
In Stock

Gaio Secondo, Plinio. Historia naturale di G. Plinio Secondo, Tradotta per M. Lodovico Domenichi con le postille in margine, Nelle quali , o vengono segnate le cose notabili, o citati altri Auttori [...]. In Venetia, Appresso Alessandro Griffio, 1580.

NewCondition € 1500.00
In Stock

Niccolò, Tommaseo. Nuovo Dizionario dei Sinonimi della lingua italiana. Milano, Per Giuseppe Rejna, 1859.

NewCondition € 350.00
In Stock

Appianus. Appiano, di Alessandria - Claude, de Seyssel - Philippe, Des Avenelles. Des guerres des Romains Livres XI traduicts en francois par seu Maistre Claude de Seyssel...Des histoires Romaines. A Paris, Par Pierre du Pré, 1569.

NewCondition € 2000.00
In Stock

Sesto Empirico. Adversus mathematicos, hoc est, adversus eos qui profitentur disciplinas, opus eruditissimum ... Eiusdem Sexti Pyrrhoniarum hypotypōseōn libri tres: ... Graecè nunquam, Latinè nunc primùm editi. Parisiis, Apud Martinum Iuvenem, 1569.

NewCondition € 3700.00
In Stock

Ernst, von Malortie. Das Menu. Eine culinarische Studie. Hannover, Klindworth’s Verlag, [1878].

NewCondition € 380.00
In Stock

Enrico, Cavacchioli Futurista. 1912. Cavalcando il Sole Versi Liberi. (Prima edizioni di soli 12 esemplari).

NewCondition € 2200.00
In Stock

Joseph of Exeter. Giuseppe, Iscano. [erroneamente Dictys Cretensis, Dares Phrygius]. Tommaso, Porcacchi. Ditte Candiotto et Darete Frigio Della Guerra Troiana, [...] [...]. In Vinegia, apresso Gabriel Giolito di Ferrari, 1570.

NewCondition € 1450.00
In Stock

Luigi, Lanzi. Storia pittorica della Italia. Dal Risorgimento delle belle Arti fin presso al fine del XVIII secolo. In Bassano, Presso Giuseppe Remondini e figli, 1809.

NewCondition € 900.00
In Stock

Niccolò de Quattrociocchi of El Borracho. Love and Dishes. New York, The Bobbs.-Merrill Company, 1950. Autografato. (VENDUTO)

NewCondition € 0.00
In Stock

Jonathan, SWIFT. Voyages de Gulliver…illustrations de A. Robida. Paris, Henri Laurens éditeur, 1928.

NewCondition € 250.00
In Stock

Anatole, France. La Rotisserie de la Reine Pédauque illustre par Auguste Leroux de 176 coimposition gravees par Duplessis, Ernest Florian, Les Deux Froment Gusman et Perrichon. Paris, Editions d’ Art Edouard Pelletan, 1911. Autografata.

NewCondition € 980.00
In Stock

Francesco Giuseppe, Gardini. De influxu Electricitatis Atmosphaericae in vegetantia dissertatio. Augustae Taurinorum, Excudebat Joannes Michael Briolus,1784.

NewCondition € 980.00
In Stock

Aristotle (Aristotele). William, Wilkinson. Aristotelis ethicorum Nichomacheorum libri decem, Codicum MSS collatione recogniti et notis illustrati, a Guilielmo Wilkinson. 1716.

NewCondition € 1600.00
In Stock

Folchino, Schizzi. Sulle sostanze nutritive che contengono le ossa, sul modo d’ estrarle col sussidio del vapore e d’ usarne a vantaggio de’ poveri […], con tavole. Milano, Per Gaspare Truffi, 1830.

NewCondition € 650.00
In Stock

Platone. Marsilio, Ficino. Omnia Divini Platonis Opera Tralatione Marsilii Ficini, Emendatione et ad graecum codicem collatione Simonis Grynaei, Nunc recens summa diligentia, quibus subiuntus est index uberrimus. 1539.

NewCondition € 5500.00
In Stock

Alexandre Frédéric Jacques, de MASSON Marquis de PEZAY. Zelis au bain, poeme en quatre chants. A Geneve, [1763].

NewCondition € 1250.00
In Stock

(a cura di Giuseppe, Galeazzi). Farmacopea ad uso de’ poveri. Veduta e riveduta dall’ Autore, ed accresciuta di una nuova Aggiunta. Milano, Presso Giuseppe Galvazzi, 1804.

NewCondition € 130.00
In Stock

Platone. Marsilio, Ficino. Omnia Divini Platonis Opera tralatione Marsilii Ficini, emendatione et ad graecum codicem collatione Simonis Grynaei nunc recens summa diligentia repurgata. 1532.

NewCondition € 6700.00
In Stock

Publio Virgilio Marone. L’ opere di Virgilio mantovano. Cioè, la Bucolica, la Georgica, e l’ Eneide, commentate in lingua volgare toscana. In Venezia, Nella Stamperia Baglioni, 1741.

NewCondition € 480.00
In Stock

James Matthew, Barrie. Peter Pan in Kensington Gardens from the little White Bird by J.M. Barrie. Illustrated by Arthur Rackham. London, Hodder & Stoughton Limited, [1912].

NewCondition € 580.00
In Stock

Sesto Rufo Festo. Epitoma de gestis et assequuto dominio romanorum. Polybii Historiarum libri quinque, nicolao perotto interprete. Basileae, Excudebat Henricus Petrus, mense marctio an. 1530.

NewCondition € 1100.00
In Stock

Carlo, Denina. Delle Rivoluzioni d' Italia libri venticinque. 1823.

NewCondition € 380.00
In Stock

Massimo, D’ Azeglio. Scritti postumi a cura di Matteo Ricci. La Lega Lombarda. Scritti Politici. Scrittori Vari. Epistolario. Firenze, G. Barbera, 1872.

NewCondition € 75.00
In Stock

Giovanni Francesco, CAMENI. Dialogorum libri quatuor, in quorum primo, qui Theophanes inscribitur, de Deo ac Trinitate precipue agitur, mox de Praedestinatione, [...]

NewCondition € 2500.00
In Stock

Johann Christopher, KOLHANS. Tractatus opticus, qui res quâm plurimas, utiles, jucundas, ludricas, & admirandas, naturalis sistere docet, nec non vitra, specula, tubosque opticos parandi 6 conficiendi rationes describit, ex optimis.

NewCondition € 1500.00
In Stock

Filippo, BUONANNI (BONANNI). Ricreatione dell' Occhio e della Mente Nell' Osservation delle Chiocciole. [...]

NewCondition € 3300.00
In Stock

Johan, Van Heurne - Ippocrate. Hippocratis coi aphorismi. Rudolphopoli, Ex Officina Freyschmidiana, 1671.

NewCondition € 0.00
In Stock

Marco Tullio Cicerone. Rhetoricorum ad Herennium libri quatuor. alias, Ars nova, sine Nova rhetorica. Rhetoricorum de Inventione. Libri Duo. Alias, Ars vetus; seu Vetus rhetorica. Venetiis, Apud Ioannem Mariam Bonellum, 1564.

NewCondition € 980.00
In Stock

Esopo. David Fransz, Van Hoostraten (Hoogstratanus). Fabularum Aesopiarum Libri V. Notis illustravit in usum serenissimi principis Nassauii […]. Amstelaedami, Ex Typographia Francisci Halmae, 1701.

NewCondition € 700.00
In Stock

Luigi, Lamberti. Portolano del Mare Mediterraneo del Mar Nero e Mare di Azof. Livorno, Tipografia Stefanini, 1856.

NewCondition € 460.00
In Stock

[Ugo, Foscolo]. Opere di Ugo Foscolo. Napoli, Francesco Rossi-Romano, 1854.

NewCondition € 160.00
In Stock

Paolo, Minoli. (Cantù, 1942 – Cantù, 2004). Composizione, 1988. Serigrafia originale a colori su carta forte ritoccata a gouache con intervento di collage. 1988.

NewCondition € 280.00
In Stock

Dione Cassio, Cocceiano. Historiae romanae libri XLVI, partim integri, partim mutili, partim excerti: Io. Leonclavii studio tam aucti, quam expoliti. Fragmenta priorum XXXIV amissorum, & posteriorem XX librorum. 1592.

NewCondition € 875.00
In Stock

Conrad, Gessner. Chirurgia. De chirurgia scriptores optimi quique veteres et recentiores, plerique in Germania antehac non editi, nunc primum in unum coniuncti volumen. Tiguri, per Andream Gessnerum et Iacobum Gessnerum fratres, mense Martio 1555.

NewCondition € 6300.00
In Stock

Paolo, Medici. Riti, e costumi degli Ebrei confutati … Coll’ aggiunta di una Lettera all’ universale del Giudaismo, compilata colle riflessioni di Niccolò Sratta Già Rabbino, e poi Cattolico Romano. In Venezia, Presso Antonio Bortoli, 1740.

NewCondition € 200.00
In Stock

Microscopio tascabile. Francia XVIII secolo.

NewCondition € 750.00
In Stock

Nicolas, Goulet. (Napoleon). Fetes a l’ occasion du mariage de S.M. Napoleon empereur des francais, roi d’ Italie, avec Marie-Louise, archiduchesse d’ Autriche. A Paris, Chez L. Ch. Soyer, 1810.

NewCondition € 1200.00
In Stock

Oviliarum Opus Luculentissimu[m] et Elegantissimu[m] Hieronymi Perboni Marchionis Incisae ac Oviliaru[m] Domini. In Libros XXVI Divisum. lano, Vincenzo Meda per Giovanni Antonio da Legnano, 1533.

NewCondition € 2200.00
In Stock

H. E., Hessus. A., Da Villanova. G., Curioni. De Tuenda bona valetudine. . (Insieme con:) Arnaldo, Da VILLANOVA. Giovanni, CURIONI. Conservandae bonae valetudinis praecepta longe saluberrima...1582.

NewCondition € 3800.00
In Stock

Louis, Aleaume o Alealmus (Ludovicus, Alealmi). Poematia. S.l. N.d. ma [Paris, Aegidius Alealmus, 1585].

NewCondition € 520.00
In Stock

Torino. Torino, Roux e Favale, 1880.

NewCondition € 250.00
In Stock

Francesco, Pona. La Galeria delle Donne Celebri. In Roma, Per il Corbelletti, ad istanza di Filippo de' Rossi, 1635.

NewCondition € 240.00
In Stock

Dante, Alighieri. La Divina Commedia col commento del P. Baldassarre Lombardi ora nuovamente arricchito di molte illustrazioni edite ed inedite. In Padova, Dalla Tipografia della Minerva, 1822.

NewCondition € 1200.00
In Stock

Gio. Francesco, LO REDANO. Scherzi geniali di Gio. Francesco, LOREDANO. All signor Cavaliere Antonio Rota. 1635.

NewCondition € 320.00
In Stock

Antonio Giuseppe, Cane. De Ipecacuanha dissertatio. Augustae Taurinorum, typis Vincentii Bianco, 1809.

NewCondition € 160.00
In Stock

Domenico, Lovisato. Cenni geografico-etnografico-geologici sopra l’ Istria. Sassari, Tipografia Azuni, 1883.

NewCondition € 120.00
In Stock

Pietro Giovanni, Vastapani. De China China in synochis putribus animadversiones. Taurini, apud Guibert, et Orgeas, 1779.

NewCondition € 230.00
In Stock

Michele, PROUDNIKOFF (PRUDNIKOV). Elucubrazione all' opera Dantesca. 1856.

NewCondition € 350.00
In Stock

Giuseppe, Bartoli. La Battaglia del colle dell’ Assietta, seguita al XIX di luglio dell’ anno 1747. In Torino, nella stamperia reale, [1747].

NewCondition € 360.00
In Stock

Pietro, BEMBO. Gli Asolani di Monsignor P. Bembo. 1540.

NewCondition € 900.00
In Stock

Emilio, Salgari. Il re della prateria. Avventure illustrate da G.G. Bruno. Firenze, Bemporad & Figlio, 1901.

NewCondition € 110.00
In Stock

Emilio, Salgari. La montagna di luce. Avventure illustrate da 20 acquerelli di G. Amato. Milano, Vallardi Editore, 1936.

NewCondition € 50.00
In Stock

Stephen, Gooden. Edwar, Fitzgerald. Rubaiyat of Omar Khayyam. London, George G. Harrap, 1940. Autografato.

NewCondition € 320.00
In Stock

Piero, Gobetti. La Rivoluzione Liberale. Saggio sulla lotta politica in Italia. Bologna, Licinio Cappelli – Libraio Editore, 18 Marzo1924. Autografato.

NewCondition € 0.00
In Stock

Bartolomeo, Castelli. Lexicon medicum graeco latinum. […] Ex Hippocrate, et Galeno desumptum. Venetiis, Apud Io: Baptistae Cestari, & Franciscum Bolzettam, 1642.

NewCondition € 850.00
In Stock

Aristotele. L' ethica…tradotta in lingua vulgare fiorentina et Commentata per Bernardo Segni. 1550.

NewCondition € 1700.00
In Stock

(Davide, Bertolotti). Descrizione di Torino. Torino, Per cura di G. Pomba, 1840.

NewCondition € 750.00
In Stock

Thomas, Gray. An Elegy written in a Country Churchyard. A new edition. London, Printed for J. Dodsley, in Pall-mall, 1771.

NewCondition € 1350.00
In Stock

Mariano, Guarani. Jus feudale neapolitanum, ac siculum. Neapoli, ex Typographia Simoniana, 1792-1794.

NewCondition € 300.00
In Stock

Dr. Hermann, Welcker. Untersuchungen über wachsthum und bau des menschlichen schädels. Leipzig, verlag von Wilhelm Engelmann, 1862.

NewCondition € 480.00
In Stock

Camillo, Benso conte di Cavour. Lettera Autografa: Modifiche al canale Carlo Alberto e costruzione del nuovo canale De Ferrari. 30 Aprile, (Metà '800 ?).

NewCondition € 950.00
In Stock

Carta Executoria de Hidalguia de Don Jeronimo de Soria.

NewCondition € 3200.00
In Stock

Camillo, Benso conte di Cavour. Lettera Autografa: Modifiche al canale Carlo Alberto e costruzione del nuovo canale De Ferrari. S.d. ma metà '800.

NewCondition € 950.00
In Stock

Luigi, Motta. Il vendicatore di Brahama Romanzo d’ avventure illustrato dal pittore Gennaro Amato Milano, L’ Italica, 1923.

NewCondition € 30.00
In Stock

Dionisio d’ Alessandria. Pomponio Mela. De Situs orbis descriptio. Aethici Cosmographia. C.I. Solini Polyistor In Dionysii poematium Commentarij, ab Henr. Stephano scripta: necnon Annotationes eius [..]. [Parigi?/Ginevra?], Excudebat H. Stephanus, 1577.

NewCondition € 1500.00
In Stock

Valerio, Frezza. Massime, regole, et precetti Di Stato, & di Guerra, Cavati da i Libri de gli Annali, & dell’ Istorie, & dalla Vita di Giulio Agricola, Di Cornelio Tacito. Da i Panegirici di Plinio Secondo a Traiano. In Napoli, Per Tarquinio L

NewCondition € 1300.00
In Stock

Catalogo delle opere di belle arti poste in mostra nel Real Museo Borbonico nel 30 Maggio 1855. Napoli, Dalla Stamperia Reale, 1855.

NewCondition € 800.00
In Stock

Isabella, Scopoli Biasi. Libro d’ Ore. Ore Pie della sposa cristiana. Torino, Fratelli Doyen Editori, 1886.

NewCondition € 1200.00
In Stock

Donald, Mennis. The Pageant of Peking. Comprising Sixty-Six Vandyke Photogravures of Peking and Environs from Photographs by Donald Mennie Shanghai, China, S. Watson & co., february 1922.

NewCondition € 2600.00
In Stock

Rudyard, Kipling. Captains courageous a story of the grand banks. London, Macmillan and Co., 1897.

NewCondition € 650.00
In Stock

Joseph François, Michaud. (cav. Luigi, Rossi) Storia delle crociate. Milano, presso la società Tipografica de’ Classici Italiani, 1819-1826.

NewCondition € 450.00
In Stock

Andrè, Theuriet. Nos oiseaux. Aquarelles de Hector Giacomelli. Parigi, H. Launette et Compagnie Editeurs, 1886.

NewCondition € 1750.00
In Stock

(Paolo, Vergani). Della pena di morte, riveduta, illustrata, ed arricchita dall’ Autore. Lettera di un giureconsulto forestiere all’ Autore. In Milano, Nella Regia Ducal Corte, per Giuseppe Richino Malatesta, 1779.

NewCondition € 850.00
In Stock

Isidore, Plaisant. Catalogue ou description bibliographique raisonnee des livres de feu Pierre-Joseph Baudewyns. Bruxelles, P.J. De Mat, Imprimeur-Libraire de l’ Academie Royal, 1818.

NewCondition € 480.00
In Stock

Schneider & C. Materiel de cote : Obusier de 293m/m de 15 calibres sur affut a pivot central [...]. [S.l.], 1913.

NewCondition € 250.00
In Stock

Etrennes de Minerve a Adolescence. A Paris, Chez Janette Libraire, 1798.

NewCondition € 1200.00
In Stock

Wenceslaus, Trnka von Krzowitz. (Wenceslaus Trnka Z. Krzowitz o Václav Trnka). Historia cardialgiae omnis aevi observata medica continens. Vindobonae, Litteris I. D. Hörlingianis, 1785.

NewCondition € 750.00
In Stock

Louis Rene, Le Canu. Corso completo di farmacia […] versione italiana con aggiunte condotta dal D. Adolfo Targioni-Tozzetti. Firenze, Presso Giovanni Ricordi e Stefano Jouhaud, 1850-1851.

NewCondition € 320.00
In Stock

Brothers Grimm [Jakob e Wilhelm]. Snowdrop & other tales illustrated by Arthur Rackam. London, Constable & Co., 1920.

NewCondition € 0.00
In Stock

Senofonte. (Xenophon). Della vita di Cyro re de Persi tradotto in lingua toscana da Iacopo di Messer Poggio Fiorentino nuovamente impresso. Impresso in Vinegia, per Gregorio de Gregori, Adi XI Marzo 1524.

NewCondition € 1600.00
In Stock

(Manoscritto) Gnomonica, sive facultas geometrice, et arithmetice horologiae constituendi. Italia, prima metà del XVIII secolo.

NewCondition € 1850.00
In Stock

Il nuovo linguaggio de’ fiori pel gentil sesso col dizionario delle piante loro emblemi e significati la botanica a colpo d’ occhio ed un manualetto di floricoltura, norme generali per la coltivazione dei fiori. Con 50 figure miniate. Milano, (metà ‘800).

NewCondition € 200.00
In Stock

Pater Noster . “The Smallest Book in the world”. [Mainz], Museo Gutenberg et Bruxelles, Plantin, 1952.

NewCondition € 3200.00
In Stock

Plutarco di Cheronea. Vitae […] novissime post Jodocum Badius Ascensium longe diligentius repositae: maioreque diligentia castigatae cum copiosore: verioreque indice. Nec non cum Aemilii [..]. Venetiis, Melchiore Sessam & Petrus de Ravanis socios, 1

NewCondition € 7000.00
In Stock

Gaio Giulio, Fedro. (Pieter Burman). Fabularum Aesopiarum libri quinque. Cum novo commentario Petri Burmanni. Leidae, Apud Samuelem Luchtmans, 1727.

NewCondition € 600.00
In Stock

Platone. Marsilio, Ficino. Omnia divini Platonis opera tralatione Marsilii Ficini. Basileae in Officina Frobeniana, anno 1539.

NewCondition € 0.00
Out Of Stock

Plato (Platone). Marsilio, Ficino. Omnia Platonis opera Tralatione Marsilij Ficini, & ad Graecum codicem accurata castigatione. Venetiis, Apud Hieronynun Scotum,1571 (al colophon, 1570).

NewCondition € 0.00
In Stock

Giorgio, Follini. Teoria Elettrica. (insieme) Ragguaglio della guarigione di un ostinato tumore operato. (insieme) Osservazioni Fisiche sul preteso vero uomo incombustibile signor. Giuseppe Lionnet. Ivrea, Ludovico Franco, 1791.

NewCondition € 950.00
In Stock

Giusto, Fontanini. De antiquitatibus Hortae colonia etruscorum libri duo. Accedunt acta vetera, inter quae Decretum sincerum Gelasii I. ex insigni codice Vaticano. Romae, Apud Franciscum Gonzagam, 1708. (Autografato dall' Autore).

NewCondition € 2200.00
In Stock

Gioacchino, Da Fiore. Girolamo Giovannini, Da Capugnano. Vaticinia sive Prophetiae Abbatis Ioachimi & Anselmi Episcopi Marsicani (Vaticinii overo Profetie dell Abbate Gioachino & di Anselmo Vescovo di Marsico). (Insieme con): Vaticinia seu...1600.

NewCondition € 2800.00
In Stock

Decimo Iunio, GIOVENALE. Iuvenalis cum commento Ioannis Britannici. Carmen Pamphili Saxi. (Rilegato insieme con :) Tito, CALPURNIO SICULO. Calpurnii & Nemesiani poetarum Buccolicum carmen una cum commentariis Diomedis Guidalotti Bononiensis.

NewCondition € 3200.00
In Stock

Monsieur des Sablons. Louis Mayeul, Chaudon. Les Grands hommes venges, ou Examen des jugements portes par M de V., [...]. A Amsterdam & se trouve a Lyon, Chez Jean-Marie Barret, 1769.

NewCondition € 190.00
In Stock

Dante, Alighieri. La Divina Commedia Già ridotta a miglior lezione dagli Accademici della Crusca; Ed ora accresciuta di un doppio Rimario, e di tre Indici copiosissimi [...]. Filosofia nello Studio di Padova. In Padova, Presso Giuseppe Comino, 1727.

NewCondition € 1600.00
In Stock

Massimo, Di Tiro. Sermones e graeca in latinam linguam versi Cosimo Paccio Interprete. 1517.

NewCondition € 2800.00
In Stock

Tommaso, Valperga di Caluso. Principes de Philosophie pour des inities aux mathematiques. Turin, au palais de l’ Academie par Vincent Bianco, 1811.

NewCondition € 420.00
In Stock

Francesco, Redi. Experimenta circa res diversas naturales, spectatim illas, Quae ex Indiis adferuntur. (Rilegato con :) Friedrich, Lachmund. De ave diomedea dissertatio. Amsterdam, Frisium, 1674. Amsterdam, Sumptibus Andrea Frisii, 1675.

NewCondition € 1400.00
In Stock

Paulus Venetus. (Paolo, Nicoletti Veneto) (Paolo di Venezia). Tractatus summularum logice. Impressum Venetiis, per Petrum de Quarengiis Pergomensem, die 7 Novembris 1506.

NewCondition € 2600.00
In Stock

Plutarco. Plutarchus. Alcuni opusculetti (opuscoletti) de le cose morali del divino Plutarco in questa nostra lingua nuovamente tradotti. 1543.

NewCondition € 600.00
In Stock

Luigi, Motta. L’ occhio di fuoco. Romanzo d’ avventure. Milano, L’ Italica, 1923.

NewCondition € 40.00
In Stock

Storia degli orrendi terremuoti che ne mesi di Novembre e Dicembre dell’ anno MDCCLV hanno desolato Lisbona, e varie altre Città del Portogallo, della Spagna, della Francia, dell Irlanda, della Germania, dell’ Africa. In Venezia, 1756.

NewCondition € 1400.00
In Stock

Scipione, Ammirato. Discorsi sopra Cornelio Tacito, Nei quali si contiene il fiore di tutto quello, che si trova sparso ne’ libri delle attioni de Principi, e del buono o cattivo loro governo. In Padova, Presso Pauolo Franbotto, 1642.

NewCondition € 280.00
In Stock

Iustiniani Imperatoris (Giustianiano Imperatore). Iustiniani Imperatoris edicta : item Justini, Tiberii ac Leonis Augustorum Novelle constitutiones. Henrico Agylaeo interprete.

NewCondition € 1400.00
In Stock

Luigi, Motta. Gli abbandonati del Galveston. Romanzo d’ avventure. Milano, L’ Italica, 1923.

NewCondition € 40.00
In Stock

Sir. James Frank, Colier. Dental surgery and pathology. London, Longmans, Green and Co., 1923.

NewCondition € 120.00
In Stock

Edgar Allan, Poe. Edmond Dulac. Les Cloches et quelques autres poèmes. Paris, Editions d’ art Piazza, G. Kadar, 1913.

NewCondition € 980.00
In Stock

Dante, Alighieri. Commedia di Dante Alighieri con ragionamenti e note di Niccolò Tommaseo. Milano, Francesco Pagnoni, 1865.

NewCondition € 950.00
In Stock

Graham, Bartlett. Bad for good. London, Allison & Busby in associaton with Goldsboro Books, June 2022. Autografato.

NewCondition € 100.00
In Stock

Giuseppe, SANCHEZ. Le Avventure del Gigante del mare rinvenuto morto ne primi giorni di Maggio 1827, presso Otranto, città del Regno di Napoli. Storia de' Ceti estratta dall' opera del conte di Lacépéde. Napoli, Dalla Tipografia di A. Trani, 1827.

NewCondition € 900.00
In Stock

J.K., Rowling. Joanne Rowling. Harry Potter and the Order of Phoenix. London, Bloomsbury, 2003.

NewCondition € 250.00
In Stock

Leila, Mottley. Night crawling. London, Bloomsbury Publishing, June 2022. Autografato.

NewCondition € 100.00
In Stock

Giorgio, Molli l’ ex marinajo. La Marina Antica e Moderna con 320 illustrazioni ed una tavola. Genova, A. Donath Editore, 1906.

NewCondition € 110.00
In Stock

Alessandro, Manzoni. I Promessi Sposi. Storia milanese del secolo XVII…con l' aggiunta degl Inni del medesimo autore. Napoli, Giosuè Rondinella editore, 1850.

NewCondition € 380.00
In Stock

Omero. Homer. Ilias & Odissea. Et in easdem scholia, sive interpretatio Didymi Cum Latina versione accuratissima. Amstelodami, Ex Officina Elzeviriana, 1655-1656.

NewCondition € 1200.00
In Stock

Nicolas, Bocangel (Bocangelino). De morbis malignis et pestilentibus, causis, prefagijs, & medendi methodo : de remedijs insuper preservativis, Tractatus. Madriti, Apud Ludovicum Sanchez, 1600.

NewCondition € 0.00
In Stock

(Vittorio, Alfieri). Vita di Vittorio Alfieri da Asti, scritta da esso. Londra (ma Firenze, Piatti), 1807.

NewCondition € 320.00
In Stock

Omero. Giuseppe Maria, Bozzoli. L’ Odissea. Venezia, Presso Antonio Zatta e Figli, 1793-1794.

NewCondition € 290.00
In Stock

Ernest, Renan. Ma soeur Henriette. Avec illustrations d’ apres Henri Scheffer et Ary Renan. Paris, Calmann Lévy Editeur, 1899.

NewCondition € 280.00
In Stock

Carlo, Gianella. Trattato di medicina preservativa diviso in sette parti in cui brevemente si ragiona delle sei cose da’ Medici dette non naturali, e s’ insegna parimente la maniera di conservare la Sanità. In Verona, Nella Stamperia Vescovile, 1751.

NewCondition € 680.00
In Stock

Torquato, Tasso. La Gerusalemme Liberata figurata da Bernardo Castello. Con le annotazioni di Scipione Gentile, e di Giulio Guastavini, et li argomenti di Oratio Ariosti. Genova, Stampata Per Giuseppe Pavoni ad istanza di Bernardo Castello, L’ Anno 1617.

NewCondition € 6200.00
In Stock

Jacob Benignus, Winslow (Winsløw). Exposition Anatomique De La Structure Du Corps Humain. A Paris, Chez Guillaume Desprez et Jean Desessartz, 1732.

NewCondition € 1350.00
In Stock